By Teresa Lara-Meloy & Jennifer Knudsen | November 27, 2018
We have spent more than 10 years studying math argumentation in middle school, in part because early teenagers are in an interesting stage in their development of argumentation skills. While they often build arguments using examples only, and have difficulties in making deductive arguments, there is increasing research that highlights the use of examples in driving deductive arguments (Ozgur et al., 2017; Stylianides & Stylianides, 2009; Knuth, Zaslavky, & Ellis, 2017).

Many of us start out reasoning through examples—in life and in math. In life, we learn to generalize from few examples. From a very young age, a child learns that every time they throw or let go of something, the something falls. Children even investigate this from different heights, and love trying this out from the high chair. It is fruitless to attempt to explain gravity at this age, yet children are able to derive this key physics truth from the many examples they’ve tried. Of course, not all thinking from examples leads to truths. Sometimes, a child infers incorrectly that dolls are girls’ toys, and yet a counterexample (or more) can help dispel that faulty conclusion. We can use both of these everyday ways of drawing conclusions from examples to support middle schoolers in making arguments in mathematics class.
In math, let’s look at at a situation in which we have seen the use of examples to build up an argument. We pose a situation where students have to determine whether the distributive property applies to algebraic expressions and works for any value of the variable. Students often start by working from left to right and then get rid of parentheses in predictable but incorrect ways. This can lead to the question:
does 2(x + 3) = 2x + 3?
Or
does 2(x + 3) = 2x + 6?
Many students start with examples. Let’s do the same.
Then,
2(4 + 3), do what’s in the parentheses first and you get 2(7) or 2•7 = 14.
2•4 + 3, do the multiplication first and you get 8 + 3 = 11
So the first two aren’t equal. But,
2•4 + 6, do the multiplication first and you get 8 + 6 = 14
So, some of us may say, the second equality—2(x + 3) = 2x + 6— is true!
(Note: we know that students would not write it out this way. But you can help them understand the “grammar” of math by speaking in sentences such as these as you write expressions on your display.)
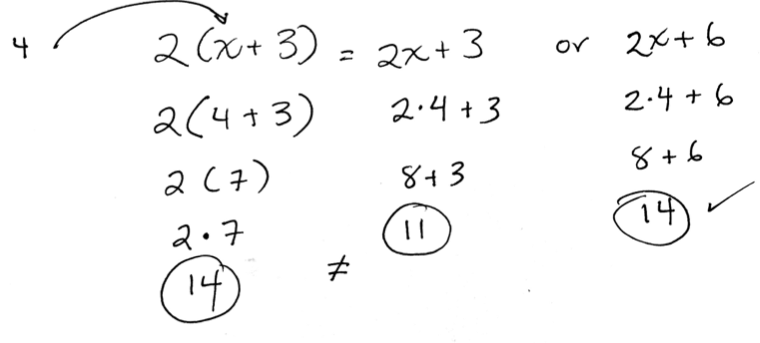
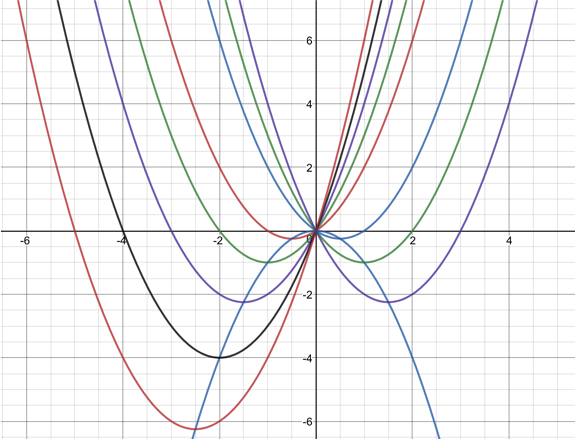
Students may stop after trying out just one number for x, or they may try out another number just to be sure. If they are being strategic in their choice of examples, they may try a negative number (to cover both sides of zero, so to speak), or they might try a large number and a small number (to see if it works for “crazy” situations). Two cases are good enough for many of us to say that the equality is always true, no matter what x is. Even many adults would stop there (e.g. Harel & Sowder, 1998; Knuth, 2002).
But as middle school math educators, we want to press for generalization—for why the second equality is always true. Or even more generally, how the distributive property works. A good diagram can help a lot in situations like these, where you want to help students generalize in algebra. You may need to give students some direction here, but you don’t need to be completely directive. Remind them of how they represented multiplication with an area model (introduced in elementary school) and ask them if they can use the same kind of diagram to help in our investigation of the distributive property. Remember algebra is generalized arithmetic! See where they take it.
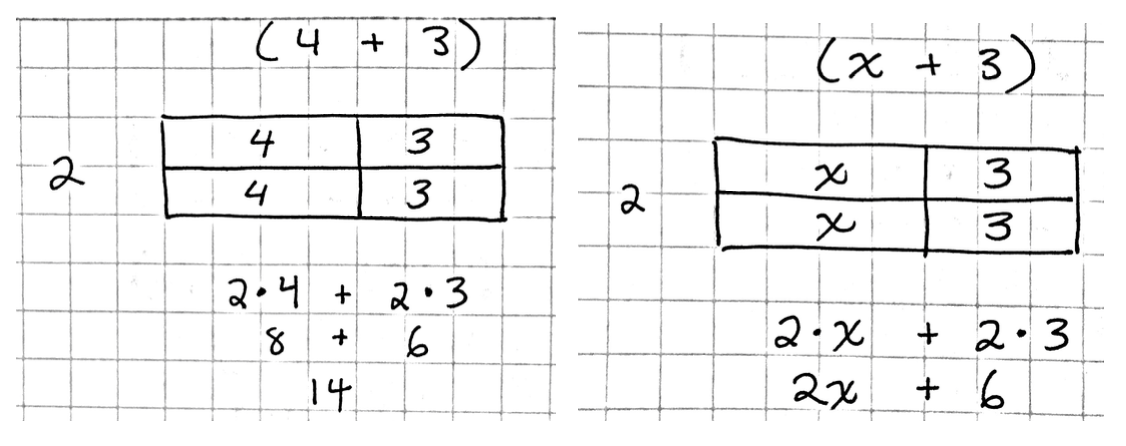
Technology can help because it allows students to better experience and represent what we mean when we say “for all x.” See what this looks like our examples above,—students can try out many substitutions for x, but it also connects with a more generalized form, which is “for all x”. Try out this GeoGebra interactive:
https://www.geogebra.org/geometry/att3e5r2
What other methods do you use to help students move from examples to generalizations? Tweet your answers with the hashtag #BridgingPD or #MathArgumentation.
You can find out more about this topic in our book, Mathematical Argumentation in Middle School.
Follow @jen_knudsen to keep up to date on our blog entries.
References
Knuth, E., Zaslavky, O., & Ellis, A. (2017). The role and use of examples in learning to prove. Journal of Mathematical Behavior (in press). Available from https://doi.org/10.1016/j.jmathb.2017.06.002
Ozgur, Z., Ellis, A. B., Vinsonhaler, R., Dogan, M. F., & Knuth, E. (2017) From examples to proof: Purposes, strategies, and affordances of example use. Journal of Mathematical Behavior (in press). Available from http://dx.doi.org/10.1016/j.jmathb.2017.03.004
Stylianides G., & Stylianides, A. (2009). Facilitating the transition from empirical arguments to proof. Journal for Research in Mathematics Education, 40 (3), 314-352.
Images
Graph: exploration of parabolas, generated by author on Desmos
Area model solutions: © SRI international