From the Book: Our Four-Part Model

Argumentation is complex and social; teachers need help implementing it in an organized way. Each part builds on the prior part, so that students build up the means to make arguments.

Equity

When argumentation is unfamiliar, the four-step model makes it approachable. Specific norms, which may be unfamiliar for math class, can be attached to each stage in the model.

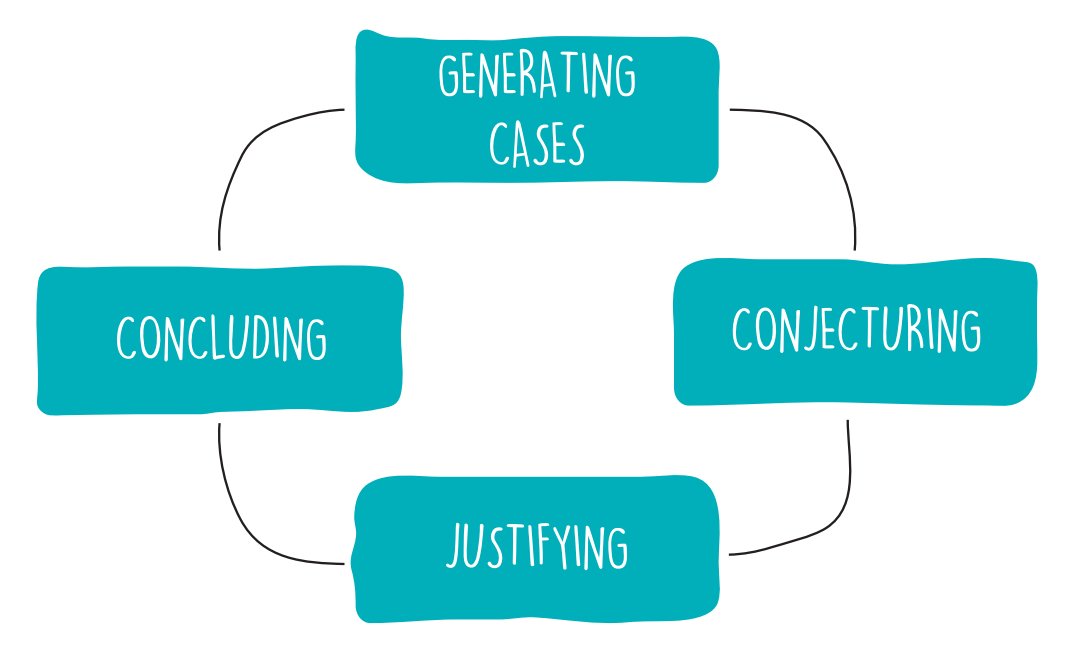
Generating Cases

When students generate cases, they create numeric expressions of geometric shapes in which they look for and examine patterns.

You need something to conjecture about!

Conjecturing

A conjecture is a mathematical statement that you think might be true.

Fundamental to argumentation
“Being right” is not required
“Make bold conjectures” is a norm
Open ended and creative

You need a specific claim to justify!

Justifying

Justifying occurs when students present reasons for why a conjecture is true or false.

A good justification convinces others. It goes beyond a personal exploration of an idea.
Comes from answering why questions- should happen all the time.
Logically connected series of statements (but won’t often come out in that order).
Representations and language are both important.

This is commonly thought of as argumentation.

Concluding

Concluding has two parts:

deciding whether a conjecture is true or false and
summarizing the justification in logical order.

Additional steps: What is the next related conjecture to explore?

Because argumentation is social, need to know when the class agrees.